ANGSD: Analysis of next generation Sequencing Data
Latest tar.gz version is (0.938/0.939 on github), see Change_log for changes, and download it here.
SFS Estimation
This method will estimate the site frequency spectrum, the method is described in Nielsen2012. The theory behind the model is briefly described here
This is a 2 step procedure first generate a ".saf" file (site allele frequency likelihood), followed by an optimization of the .saf file which will estimate the Site frequency spectrum (SFS).
For the optimization we have implemented 2 different approaches both found in the misc folder. The diagram below shows the how the method goes from raw bam files to the SFS.
You can also estimate a 2dsfs.
* NB the ancestral state needs to be supplied for the full SFS, but you can use the -fold 1 to estimate the folded SFS and then use the reference as ancestral. * NB the output from the -doSaf 2 are not sample allele frequency likelihoods but sample alle posteriors. And applying the realSFS to this output is therefore NOT the ML estimate of the SFS as described in the Nielsen 2012 paper, but the 'Incorporating deviations from Hardy-Weinberg Equilibrium (HWE)' section of that paper.
<classdiagram type="dir:LR">
[sequence data{bg:orange}]->GL[genotype likelihoods|SAMtools;GATK;SOAPsnp;Kim et.al]
[genotype likelihoods|SAMtools;GATK;SOAPsnp;Kim et.al]->doSaf[.saf file{bg:blue}] [.saf file{bg:blue}]->optimize('realSFS')[.saf.ml file{bg:red}]
</classdiagram>
Brief Overview
./angsd -doSaf -> angsd version: 0.569 build(Dec 17 2013 12:40:00) -> Analysis helpbox/synopsis information: -------------- angsd_realSFS.cpp: -doSaf 0 1: perform multisample GL estimation 2: use an inbreeding version 3: calculate genotype probabilities (beta) 4: Assume genotype posteriors as input (still beta) -doThetas 0 (calculate thetas) -underFlowProtect 0 -fold 0 (deprecated) -anc (null) (ancestral fasta) -noTrans 0 (remove transitions) -pest (null) (prior SFS)
misc/realSFS ./realSFS afile.sfs nChr [-start FNAME -P nThreads -tole tole -maxIter -nSites ] nChr is the number of chromosomes. (twice the number of diploid invididuals)
See more here: realSFS
Options
- -doSaf 1
- Calculate the Site allele frequency likelihood based on individual genotype likelihoods assuming HWE
- -doSaf 2
- (version above 0.503) Calculate per site posterior probabilities of the site allele frequencies based on individual genotype likelihoods while taking into account individual inbreeding coefficients. This is implemented by Filipe G. Vieira. You need to supply a file containing all the inbreeding coefficients. -indF
- -doSaf 3
- Calculate the posterior probabilities of the sample allele frequency distribution for each site. This needs a prior distribution of the SFS (which can be obtained from -doSaf 1/realSFS)
- -doSaf 4
- Calculate the posterior probabilities of the sample allele frequency distribution for each site based on genotype probabilities. The genotype probabilities should be provided by the using using the -beagle options. Often the genotype probabilities will be obtained by haplotype imputation.
- -underFlowProtect [INT]
0: (default) no underflow protection. 1: use underflow protection. For large data sets (large number of individuals) underflow projection is needed.
Example
A full example is shown below where we use the test data that can be found on the quick start page. In this example we use GATK genotype likelihoods.
first generate .saf file with 4 threads
./angsd -bam bam.filelist -doSaf 1 -out small -anc chimpHg19.fa -GL 2 -P 4
We always recommend that you filter out the bad qscore bases and meaningless mapQ reads. eg -minMapQ 1 -minQ 20. So the above analysis with these filters can be written as:
./angsd -bam bam.filelist -doSaf 1 -out small -anc chimpHg19.fa -GL 2 -P 4 -minMapQ 1 -minQ 20
Obtain a maximum likelihood estimate of the SFS using EM algorithm
misc/realSFS small.saf 20 -maxIter 100 -P 4 >small.sfs
What does the 20 mean in the realSFS command? This is the number of chromosomes
- If you have say 10 diploid samples, then you should choose 20
- if you have say 12 diploid samples, then you should choose 24.
- If you have say 14 diploid samples, and you fold the spectrum then you should choose 28
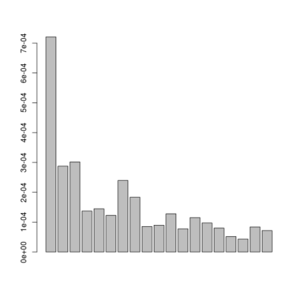
A plot of this figure are seen on the right. The jaggedness is due to the very low number of sites in this small dataset.
Interpretation of the output file
The output from realSFS (small.sfs) is the SFS in logscale. This is to be interpreted as:
column1 := probabilty of sampling zero derived alleles (on logscale)
column2 := probabilty of sampling one derived allele (on logscale)
column3 := probabilty of sampling two derived allele (on logscale)
column4 := probabilty of sampling three derived allele (on logscale)
etc
each row is a region of the genome (see below).
NB
The generation of the .saf file contains a saf for each site, whereas the optimization requires information for a region of the genome. The optimization will therefore use large amounts of memory.
Folded spectra
If you don't have the ancestral state, you can instead estimate the folded SFS. This is done by supplying the -anc with the reference genome and also supply -fold 1. Then you should remember to change the second parameter to the realSFS function as the number of individuals instead of the number of chromosomes.
The above example would then be
#first generate .saf file
./angsd -bam bam.filelist -doSaf 1 -out smallFolded -anc chimpHg19.fa -GL 2 -fold 1
#now try the EM optimization with 4 threads
misc/realSFS smallFolded.saf 10 -maxIter 100 -P 4 >smallFolded.sfs
#in R
sfs<-exp(scan("smallFolded.sfs"))
barplot(sfs[-1])
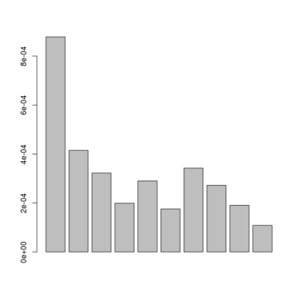
Posterior of the per-site distributions of the sample allele frequency
If you supply a prior for the SFS (which can be obtained from the -doSaf/realSFS analysis), the output of the .saf file will no longer be site allele frequency likelihoods but instead will be the log posterior probability of the sample allele frequency for each site.
Format specification of binary .saf file
The information in this section is only usefull for people who wants to work with the "multisample GL"/"sample allele frequencies" for the individual sites.
Assuming 'n' individuals we have (2n+1) categories for each site, each value is encoded as ctype double which on 'all known' platforms occupies 8 bytes. The (2n+1) values are log scaled like ratios, which means that the most likely category will have a value of 0.
The information for the first site is the first (2n+1)sizeof(double) bytes. The information for the next site is the next (2n+1) bytes etc. The positions are given by the ascii file called '.saf.pos'
#sample code to read .saf in c/c++ assuming 10 individuals
FILE *fp = fopen("mySFS.saf","rb");
int nInd = 10;
double persite[2*nInd+1];
fread(persite,sizeof(double)*(2*nInd+1),1,fp);
for(int i=0;i<2*nind+1;i++)
fprintf(stderr,"cat: %d = %f\n",i,persite[i]);
- If the -fold 1 has been set, then the dimension is no longer 2*nInd+1 but nInd+1
- If the -pest parameter has been supplied the output is no longer likelihoods but log posterior site allele frequencies
How to plot
Assuming the we have obtained a single global sfs(only one line in the output) from realSFS program, and this is located in file.saf.sfs, then we can plot the results simply like:
sfs<-exp(scan("small.sfs")) #read in the log sfs
barplot(sfs[-c(1,length(sfs))]) #plot variable sites

We can make it more fancy like below:
#function to normalize
norm <- function(x) x/sum(x)
#read data
sfs <- exp(scan("small.sfs"))
#the variability as percentile
pvar<- (1-sfs[1]-sfs[length(sfs)])*100
#the variable categories of the sfs
sfs<-norm(sfs[-c(1,length(sfs))])
barplot(sfs,legend=paste("Variability:= ",round(pvar,3),"%"),xlab="Chromosomes",
names=1:length(sfs),ylab="Proportions",main="mySFS plot",col='blue')
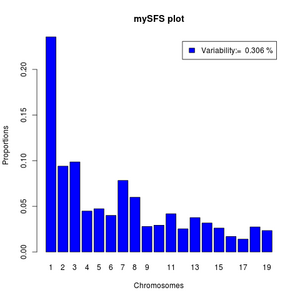
If your output from realSFS contains more than one line, it is because you have estimated multiple local SFS's. Then you can't use the above commands directly but should first pick a specific row.
sfs<-exp(as.numeric(read.table("multiple.sfs")[1,])) #first region.
#do the above
sfs<-exp(as.numeric(read.table("multiple.sfs")[2,])) #second region.
Which genotype likelihood model should I choose ?
It depends on the data. As shown on this example Glcomparison, there was a huge difference between -GL 1 and -GL 2 for older 1000genomes BAM files, but little difference for newer bam files.
Validation
-doSaf 1
cd misc;
./supersim -outfiles test -npop 1 -nind 12 -pvar 0.9 -nsites 50000
echo testchr1 100000 >test.fai
../angsd -fai test.fai -glf test.glf.gz -nind 12 -doSaf 1 -issim 1
./realSFS angsdput.saf 24 2>/dev/null >res
R -q
exp(scan("res"))-scan("test.frq")
Read 25 items
Read 25 items
[1] -2.717005e-04 -5.709517e-04 1.531743e-03 -7.544274e-05 -1.142167e-03
[6] 1.260423e-04 8.145499e-04 -8.061657e-04 6.044666e-04 3.458799e-04
[11] -1.212797e-04 -3.164292e-04 -3.959988e-04 4.962791e-04 -5.113052e-04
[16] 6.739867e-04 -8.682795e-04 5.458678e-04 -3.403997e-04 7.917004e-04
[21] -2.430954e-04 -1.863518e-04 -1.639591e-04 3.044223e-04 -2.217054e-04
-doSaf 2
ngsSim=../ngsSim/ngsSim
angsd=./angsd
realSFS=./misc/realSFS
$ngsSim -npop 1 -nind 24 -nsites 1000000 -depth 4 -F 0.0 -outfiles testF0.0
$ngsSim -npop 1 -nind 24 -nsites 1000000 -depth 4 -F 0.9 -outfiles testF0.9
for i in `seq 24`;do echo 0.9;done >indF
echo testchr1 250000000 >test.fai
$angsd -fai test.fai -issim 1 -glf testF0.0.glf.gz -nind 24 -out noF -dosaf 1
$angsd -fai test.fai -issim 1 -glf testF0.9.glf.gz -nind 24 -out withF -dosaf 2 -domajorminor 1 -domaf 1 -indF indF
$realSFS noF.saf 48 >noF.sfs
$realSFS withF.saf 48 >withF.sfs
#in R
trueNoF<-scan("testF0.0.frq")
trueWithF<-scan("testF0.9.frq")
pdf("sfsFcomparison.pdf",width=14)
par(mfrow=c(1,2),width=14)
barplot(trueNoF[-1],main='true sfs F=0.0')
barplot(trueWithF[-1],main='true sfs F=0.9')
estWithF<-exp(scan("withF.sfs"))
estNoF<-exp(scan("noF.sfs"))
barplot(rbind(trueNoF,estNoF)[,-1],main="true vs est SFS F=0 (ML)",be=T,col=1:2)
barplot(rbind(trueWithF,estWithF)[,-1],main='true vs est sfs=0.9 (MAP)',be=T,col=1:2)
readBjoint <- function(file=NULL,nind=10,nsites=10){
ff <- gzfile(file,"rb")
m<-matrix(readBin(ff,double(),(2*nind+1)*nsites),ncol=(2*nind+1),byrow=TRUE)
close(ff)
return(m)
}
m <- exp(readBjoint("withF.saf",nind=24,5e6))
barplot(rbind(trueWithF,colMeans(m))[,-1],main='true vs est sfs F=0.9 (colmean of site pp)',be=T,col=1:2)
dev.off()