NgsAdmixv2: Difference between revisions
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
[[File:NgsAdmix.png|thumb]] | [[File:NgsAdmix.png|thumb]] | ||
The method was published in 2013 and can be found here: [http://www.ncbi.nlm.nih.gov/pubmed/24026093] | The method was published in 2013 and can be found here: [http://www.ncbi.nlm.nih.gov/pubmed/24026093] | ||
Citation: Skotte, Line et al. “Estimating individual admixture proportions from next generation sequencing data.” Genetics vol. 195,3 (2013): 693-702. doi:10.1534/genetics.113.154138 | Citation: Skotte, Line et al. “Estimating individual admixture proportions from next generation sequencing data.” Genetics vol. 195,3 (2013): 693-702. doi:10.1534/genetics.113.154138 | ||
The latest version is 32 from June 25 2013 and can be downloaded here: [http://popgen.dk/software/download/NGSadmix/ngsadmix32.cpp ]. | |||
Older versions can be found here: | |||
[http://popgen.dk/software/download/NGSadmix/]. | |||
=Installation= | =Installation= | ||
Revision as of 11:16, 21 June 2019
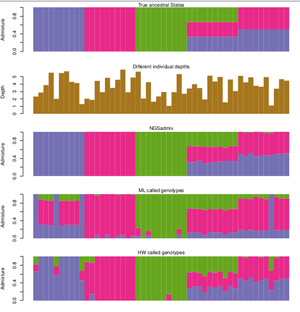
This page contains information about the program called NGSadmix, which is a very nice tool for estimating individual admixture proportions from NGS data. It is based on genotype likelihoods and works well for medium and low coverage NGS data. It is a fancy multithreaded c/c++ program. We really like it.
The method was published in 2013 and can be found here: [1]
Citation: Skotte, Line et al. “Estimating individual admixture proportions from next generation sequencing data.” Genetics vol. 195,3 (2013): 693-702. doi:10.1534/genetics.113.154138
The latest version is 32 from June 25 2013 and can be downloaded here: [2].
Older versions can be found here: [3].
Installation
wget popgen.dk/software/download/NGSadmix/ngsadmix32.cpp g++ ngsadmix32.cpp -O3 -lpthread -lz -o NGSadmix
Brief Overview
./NGSadmix
Arguments: -likes Beagle likelihood filename -K Number of ancestral populations Optional: -fname Ancestral population frequencies -qname Admixture proportions -outfiles Prefix for output files -printInfo print ID and mean maf for the SNPs that were analysed Setup: -seed Seed for initial guess in EM -P Number of threads -method If 0 no acceleration of EM algorithm -misTol Tolerance for considering site as missing Stop chriteria: -tolLike50 Loglikelihood difference in 50 iterations -tol Tolerance for convergence -dymBound Use dymamic boundaries (1: yes (default) 0: no) -maxiter Maximum number of EM iterations Filtering -minMaf Minimum minor allele frequency -minLrt Minimum likelihood ratio value for maf>0 -minInd Minumum number of informative individuals
NB All parameters are set using -par value. So to get additional information you would write -printInfo 1.
Run example
First download some example test files which has been generated on basis of data from the 1000 genomes project (100 individuals from 5 populations with 50000 SNPs).
wget popgen.dk/software/download/NGSadmix/data/input.gz wget popgen.dk/software/download/NGSadmix/data/pop.info
We then have an input file called input.gz and assuming 3 ancestral populations (-K 3), and that we want to use 4 computing cores (-P 4). The prefix of the output files is myoutfiles (-o myoutfiles) using only SNP with af MAF above 5% (-minMaf 0.05).
./NGSadmix -likes input.gz -K 3 -P 4 -o myoutfiles -minMaf 0.05
-> Dumping file: myoutfiles.log -> Dumping file: myoutfiles.filter Input: lname=input.gz nPop=3, fname=(null) qname=(null) outfiles=myoutfiles Setup: seed=1374071670 nThreads=4 method=1 Convergence: maxIter=2000 tol=0.000010 tolLike50=0.100000 dymBound=0 Filters: misTol=0.050000 minMaf=0.050000 minLrt=0.000000 minInd=0 Input file has dim: nsites=50000 nind=100 Input file has dim (AFTER filtering): nsites=49475 nind=100 iter[start] like is=6395247.407627 iter[50] like is=-3868746.751237 thres=0.002523 iter[100] like is=-3866294.760777 thres=0.003179 iter[150] like is=-3865984.169517 thres=0.000310 iter[200] like is=-3865965.879519 thres=0.000017 EM accelerated Thread has reached convergence with tol 0.000010 best like=-3865964.425455 after 245 iterations -> Dumping file: myoutfiles.qopt -> Dumping file: myoutfiles.fopt.gz [ALL done] cpu-time used = 211.93 sec [ALL done] walltime used = 105.00 sec
Input Files
Input files are contains genotype likelihoods in genotype likelihood beagle input file format [4]. We recommend ANGSD for easy transformation of Next-generation sequencing data to beagle format. See Creation of Beagle files with ANGSD
Example of a beagle genotype likelihood input file for 3 individuals.
marker allele1 allele2 Ind0 Ind0 Ind0 Ind1 Ind1 Ind1 Ind2 Ind2 Ind2 1_14000023 1 0 0.941 0.058 0.000 0.799 0.199 0.001 0.666 0.333 0.001 1_14000072 2 3 0.709 0.177 0.112 0.941 0.058 0.000 0.665 0.332 0.001 1_14000113 0 2 0.855 0.106 0.037 0.333 0.333 0.333 0.799 0.199 0.000 1_14000202 2 0 0.835 0.104 0.060 0.799 0.199 0.000 0.333 0.333 0.333 ...
Column 1:The marker name (the information is not atually used)
Column 2 and 3: the major and minor allele (these two columns are not used within the program and can contain whatever dummy value).
The rest of the colums are the genotypes likelihoods (not in log space). For each individual we have 3 columns. Note that the above values sum to one per sites for each individuals. This is just a normalization of the genotype likelihoods in order to avoid underflow problems in the beagle software it does not mean that they are genotype probabilities.
The input file is allowed to be compressed with gzip.
Options
./NGSadmix Arguments: -likes Beagle likelihood filename -K Number of ancestral populations Optional: -fname Ancestral population frequencies -qname Admixture proportions -o Prefix for output files -printInfo print ID and mean maf for the SNPs that were analysed Setup: -seed Seed for initial guess in EM -P Number of threads -method If 0 no acceleration of EM algorithm -misTol Tolerance for considering site as missing Stop chriteria: -tolLike50 Loglikelihood difference in 50 iterations -tol Tolerance for convergence -dymBound Use dymamic boundaries (1: yes (default) 0: no) -maxiter Maximum number of EM iterations Filtering -minMaf Minimum minor allele frequency -minLrt Minimum likelihood ratio value for maf>0 -minInd Minumum number of informative individuals
Output Files
Program outputs 3 files.
- PREFIX.log
- PREFIX.fopt.gz
- PREFIX.qopt
- The .log file contains log information of the run. Commandline used for running the program, what the likelihood is every 50 iterations, and finally how long it took to do the run.
- The .fopt.gz file is an compressed file, which contains an estimate of the frequency for each site for all populations.
- The .qopt file contains the admixture proportions for all individuals.
Examples of the output files are found below.
Log file (.log)
Contents of the file log file
-> Dumping file: tskSim/tsk6GL.beagle.s1.log -> Dumping file: tskSim/tsk6GL.beagle.s1.filter Input: lname=tskSim/tsk6GL.beagle nPop=3, fname=(null) qname=(null) outfiles=tskSim/tsk6GL.beagle.s1 Setup: seed=1 nThreads=10 method=1 Convergence: maxIter=2000 tol=0.000000 tolLike50=0.010000 dymBound=0 Filters: misTol=0.050000 minMaf=0.000000 minLrt=0.000000 minInd=0 Input file has dim: nsites=100000 nind=75 Input file has dim (AFTER filtering): nsites=100000 nind=75 iter[start] like is=9299805.984931 iter[50] like is=-6531138.892608 thres=0.002800 iter[100] like is=-6528710.773349 thres=0.001289 iter[150] like is=-6528405.896951 thres=0.001211 iter[200] like is=-6528306.803820 thres=0.000420 iter[250] like is=-6528277.160993 thres=0.000546 iter[300] like is=-6528271.925055 thres=0.000033 iter[350] like is=-6528271.177692 thres=0.000008 iter[400] like is=-6528270.876315 thres=0.000005 iter[450] like is=-6528270.772894 thres=0.000140 iter[500] like is=-6528270.747721 thres=0.000002 iter[550] like is=-6528270.740654 thres=0.000002 Convergence achived because log likelihooditer difference for 50 iteraction is less than 0.010000 best like=-6528270.740654 after 550 iterations -> Dumping file: tskSim/tsk6GL.beagle.s1.qopt -> Dumping file: tskSim/tsk6GL.beagle.s1.fopt.gz [ALL done] cpu-time used = 671.82 sec [ALL done] walltime used = 114.00 sec
Allele frequency ouput (.fopt)
Each column correponds to the estimated allele frequencies for each population and each line is a SNP
Example of a .fopt file for -K 3
... 0.75331646167520038837 0.51190946588401886608 0.50134051056701267601 0.99999999900000002828 0.80165850924934911603 0.97470665326916294813 0.99999999900000002828 0.89560828888972687789 0.88062641752218895341 0.99999999900000002828 0.99999999900000002828 0.86109994249930577048 0.70560445653074521655 0.78994686954000448154 0.93076614062025020413 0.99999999900000002828 0.88878537780630872955 0.92662857068149151463 0.05322676762098016434 0.22871739860812340117 0.17394852600322696645 0.00000000100000000000 0.27428885137150410545 0.19029599645013275944 0.57086006389212373691 0.42232596591112880891 0.74080063581586474974 0.77359733910003525281 0.47380864146016693494 0.72073560889718923939 0.49946404159405927148 0.21684946347150244050 0.15201985942558055021 0.41802171086717271331 0.55490556205954566504 0.85691127728452165524 0.77095213528720529794 0.60074618451005279418 0.70219544996184157792 0.26517850405564091787 0.48500265408436060710 0.85432254709914456914 0.80055081986260245852 0.74423201242010783574 0.87110476762969968334 0.30563054476851375663 0.05233529475348827620 0.25911912824038613179 0.51084997710733415222 0.62263692178557350498 0.50738250264097506381 0.64790272562679740442 0.91230541484222271720 0.73015721390331478347 0.07124629651164265942 0.37896482494356753534 0.29218012479334326548 0.00000000100000000000 0.26969100790961914038 0.28395781874856029781 0.97074775756045073027 0.79093498372643300520 0.64006920058897498471 0.64661948716978157048 0.84130009558421925409 0.76730057769159087933 0.86990900887920663553 0.79410745692063922085 0.69416721874359499367 0.34956069940263900797 0.27773038429396151860 0.25923476721423144298 0.77739744690560164120 0.51272232330145017798 0.53888718200036844763 0.35431569298041332150 0.20022780744715171219 0.43176580786072032980 0.91858160919413811563 0.99999999900000002828 0.93584179237779097082 0.90339823126358831384 0.94729687041528465308 0.84358671720630329371 0.87068129661127857677 0.65267891763324525911 0.59315740612546075106 0.24102496839012735319 0.42777100607917967201 0.39594098602469629533 0.99999999900000002828 0.99999999900000002828 0.78549330115836857313 0.15386277372522660922 0.18035502891341426146 0.26583557049163752950 0.22456748943597096280 0.25110807159057474403 0.17244618960511531869 0.74816053649164548922 0.54769319158907958656 0.44532166240679449398 0.76350303696805599252 0.86547244122202959815 0.94111974586621383043 0.40940400475566068872 0.67767095908245833513 0.40793761498610620064 0.85389765162910868934 0.78901563183853873351 0.93614065916219291186 0.54108661985898742763 0.61895909938546000983 0.88522763262549941654 0.99051495581855464323 0.78855843624128341141 0.77646441702623147929 0.51133721761171413434 0.74521610846562824637 0.32689774480116673416 0.66618479413060949224 0.67891474309775079465 0.80762116232856140385 0.81793598261160704865 0.77752326447671193943 0.95349025244041396565 0.82120324647844433752 0.99999999900000002828 0.89800731971059466474 ...
Use the "-printInfo 1" option to get the position of the lines in the fopt file if some sites have been flltered from the analysis (-minMaf, minInd, minLRT etc)
Admixture proportion output file (.qopt)
Infered admixture proporsions. Each line is an individual and each column is a population.
Contents of the qopt file # cat tsk48GL.beagle.gz.s1.qopt
0.00254460532103031574 0.00108987228478324210 0.99636552239418640919 0.00000015905647541105 0.00000000100000000000 0.99999983994352459327 0.00034770382567266174 0.02639209238328452459 0.97326020379104283275 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000467398081877176 0.00000000100000000000 0.99999532501918120264 0.00000000907496942853 0.00585150933779484805 0.99414848158723567728 0.00515826525767644137 0.01138897436535154552 0.98345276037697204607 0.03914841746468285949 0.00000000100000000000 0.96085158153531713410 0.00000000100000000000 0.00629199375758324100 0.99370800524241675866 0.00771173022930659625 0.00000154720357311662 0.99228672256712036059 0.00000000100000000000 0.00075135345721917719 0.99924864554278081119 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000005468413042120 0.00087279924180633879 0.99912714607406327705 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00712941313019542066 0.00118955677574110528 0.99168103009406338710 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00165385222968000606 0.99834614677032007535 0.00000000100000000000 0.00006297763597355473 0.99993702136402651259 0.00519087111391381209 0.00000000100000000000 0.99480912788608621966 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00202872783596746379 0.00000000100000000000 0.99797127116403261393 0.00876424336999809782 0.00949457841911990376 0.98174117821088191516 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.01820430093358888640 0.00000694033297829119 0.98178875873343274261 0.00351013812443964728 0.00000020340562512923 0.99648965846993520223 0.00771897550085272680 0.00605259705033356268 0.98622842744881378252 0.00600595292580561029 0.00000000100000000000 0.99399404607419439284 0.01454910070242997067 0.00543457657939076105 0.98001632271817917808 0.02567862615486414535 0.00160921436783232220 0.97271215947730349516 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00001041560507852223 0.99998958339492149960 0.00000000100000000000 0.01383432553657116572 0.98616567346342876021 0.00343840097404925389 0.00000000100000000000 0.99656159802595079000 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00051244065751142103 0.00404846039501185508 0.99543909894747661937 0.02003953974792894652 0.00000004934009128878 0.97996041091197982897 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.02176809890633762956 0.00000000100000000000 0.97823190009366245423 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.01563096189267457192 0.00970868396771427770 0.97466035413961116252 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00002540964943070735 0.00000000100000000000 0.99997458935056915408 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99501476026684787524 0.00000000100000000000 0.00498523873315206718 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99520671498720802983 0.00479241730266987201 0.00000086771012207898 0.95884374919730619435 0.00000000100000000000 0.04115624980269377842 0.99002104218586972628 0.00000000100000000000 0.00997895681413022567 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999770925251941 0.00000000129074746013 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.98980053177767901573 0.00000005577971952226 0.01019941244260143612 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999785004878083416 0.00000000100000000000 0.00000214895121910354 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99220030909132039820 0.00000000100000000000 0.00779968990867968733 0.99999996788621803301 0.00000000100000000000 0.00000003111378189772 0.99736783433174225344 0.00255940950853666971 0.00007275615972113173 0.99998096423035520708 0.00000000574461213317 0.00001903002503262207 0.99711097909957713270 0.00288887008493822353 0.00000015081548462101 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99769262012085335734 0.00000000100000000000 0.00230737887914652393 0.99999820787375570674 0.00000000433914936351 0.00000178778709493472 0.98047422489554170166 0.00012980111977614777 0.01939597398468214523 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.98208006049140339488 0.00000000100000000000 0.01791993850859651197 0.97530298545159921364 0.00000000100000000000 0.02469701354840085974 0.99657542812406740840 0.00000000100000000000 0.00342457087593254226 0.99954556420189066834 0.00045443479810919004 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99531584565237773976 0.00410740812985130408 0.00057674621777084644 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99878572597704817770 0.00000000100000000000 0.00121427302295177490 0.98571687209123504125 0.00400077401169816448 0.01028235389706666329 0.99027397554762419674 0.00840892511494516215 0.00131709933743062008 0.99999993504923445631 0.00000000100000000000 0.00000006395076564386 0.95946639819101930957 0.00000000100000000000 0.04053360080898076034 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.98414939425022363029 0.01585059024074651421 0.00000001550902978739 0.99999999622245250297 0.00000000277754757396 0.00000000100000000000 0.99525652466242930938 0.00000001683386219288 0.00474345850370842034 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999965447943561792 0.00000000100000000000 0.00000034452056438734 0.99864814059528783652 0.00135185840471215468 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000001076370464123 0.99999998823629543399 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000 0.99999986659623718577 0.00000013240376283687 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999 0.00000000100000000000 0.99632783404679736705 0.00367216495320256799 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999 0.35919621347731411909 0.32381633362411937904 0.31698745289856661289 0.31048363757756514136 0.30902410742704566893 0.38049225499538924522 0.36341140678787386964 0.33678307361394943520 0.29980551959817652863 0.34550713774447228133 0.34037087985425079628 0.31412198240127681137 0.34705579219215104692 0.35218792485566730033 0.30075628295218165276 0.33646039412306782967 0.32632754139618752598 0.33721206448074481088 0.31881401220765009930 0.34885621407165418040 0.33232977372069577582 0.34999374672052624424 0.33030931848049555066 0.31969693479897826061 0.33152251818028721786 0.32339147992992234304 0.34508600188979043910 0.31959998197389311025 0.33152491237148390413 0.34887510565462298562 0.34724548642936803322 0.31809475756470984020 0.33465975600592196004 0.33378069767858009609 0.33223636639277298599 0.33398293592864686241 0.32023090400419051971 0.33179989332826043125 0.34796920266754916007 0.35205158009776410521 0.33547091017851976558 0.31247750972371612921 0.34291063455495451873 0.31853488093100223999 0.33855448451404313026 0.31929132670383747472 0.32755905579808902717 0.35314961749807355362 0.34114474726121107873 0.34607065583774476725 0.31278459690104404300 0.33725705347681012025 0.32910919226619778089 0.33363375425699209886 0.33918213722968154622 0.32278745806952213737 0.33803040470079642743 0.33788659799509024317 0.34692305448657090317 0.31519034751833896468 0.35876135180876589370 0.33843260979944000955 0.30280603839179404124 0.34721570614318736370 0.34395335873604998556 0.30883093512076259524 0.34165097731337079612 0.32814110943000784903 0.33020791325662146587 0.33922542743931027864 0.32639619830977489867 0.33437837425091476717 0.34461619391735059947 0.33133174331942943924 0.32405206276321996128 0.34277551565686120716 0.32746953398981676342 0.32975495035332202942 0.33842982221926010133 0.31224638933762871584 0.34932378844311123833 0.34443810815667752490 0.32640113997211872565 0.32916075187120380496 0.31723258569943768581 0.34955203711397470068 0.33321537718658750249 0.35394053250677920408 0.33291498389624818444 0.31314448359697255597 0.33504517457864940733 0.34188143503173562543 0.32307339038961496724 0.33240938202788244960 0.34671459781042585080 0.32087602016169164409 0.31745792352948248860 0.33722730677636020280 0.34531476969415725309 0.33098224522913716195 0.33312298285105168549 0.33589477191981131909 0.34090909280056919117 0.32423671881295645925 0.33485418838647434958 0.32985465610121944557 0.32124851771265583444 0.34889682618612483100 0.33525528582568764335 0.31967441393853385234 0.34507030023577844879 0.33823045943274382408 0.33932114218381809190 0.32244839838343819505 0.34374166546335593875 0.33527470302709477812 0.32098363150954922762 0.32177399566214615056 0.34277626859597382092 0.33544973574188002852 0.34915111840878915173 0.33072079898488659921 0.32012808260632419355 0.31132788816691708833 0.32844185942225745389 0.36023025241082540227 0.33067206673512555826 0.34601992411426535368 0.32330800915060908807 0.31337643746173032833 0.33835721859074846529 0.34826634394752131740 0.32762993090356395953 0.34856645453438306337 0.32380361456205303261 0.33558678075595765877 0.34449062515269568419 0.31992259409134682357 0.33433652456352996873 0.32868556951924504661 0.33697790591722515119 0.32115036446030281736 0.35050069566489522321 0.32834893987480190392 0.32524569843140932468 0.33953480032298033464 0.33521950124561045170 0.33520046917246110185 0.31124301814705779279 0.35355651268048110536 0.51565151014669796670 0.00027180960956305278 0.48407668024373901039 0.51978922685130035664 0.01333903580405943964 0.46687173734464021413 0.48123878312258933088 0.00648941795451128591 0.51227179892289931296 0.48941833241028537271 0.00512373007237581363 0.50545793751733880672 0.48421136927686320162 0.00600153379448644612 0.50978709692865020742 0.53246468447754891073 0.00000000100000000000 0.46753531452245111755 0.50637710620505416159 0.01564455874020675985 0.47797833505473913407 0.49416813414210103428 0.00000000100000000000 0.50583186485789899400 0.51328206693115174808 0.00000000100000000000 0.48671793206884833571 0.50420356848059588728 0.00779539942445491366 0.48800103209494921641 0.51589943710654184716 0.00000000100000000000 0.48410056189345807010 0.46643393286795947761 0.00024627960390510270 0.53331978752813535838 0.50134326603627110686 0.00000000100000000000 0.49865673296372897694 0.52516062216154979492 0.00887494007947397384 0.46596443775897622430 0.50553300231497877437 0.00610541400596737328 0.48836158367905380118 0.48505848053244243756 0.00412236953776635561 0.51081914992979127188 0.50419106430093152404 0.00671707921410998055 0.48909185648495850929 0.51266037905765671212 0.00565931340437971983 0.48168030753796364785 0.50479638826213368841 0.00082364200405335279 0.49437996973381287402 0.48963785250324892706 0.00000000100000000000 0.51036214649675115673 0.49861342640726780129 0.00000000100000000000 0.50138657259273211597 0.49321745088202589846 0.00000000100000000000 0.50678254811797418533 0.52297921048641760056 0.00000000100000000000 0.47702078851358242773 0.51351947193443381323 0.00000000100000000000 0.48648052706556610403 0.49861600587139209839 0.01143470350387426789 0.48994929062473369097 0.47497824395255133778 0.00413641430709298184 0.52088534174035572288 0.50602874958787047444 0.00000013752429825494 0.49397111288783129845 0.51347175918678078510 0.00477133273041653854 0.48175690808280269284 0.50359809216181616875 0.00000002299679746021 0.49640188484138642044 0.52201190781479689385 0.00000000100000000000 0.47798809118520296790 0.52427554763933403859 0.01637369304678280152 0.45935075931388308357 0.50464335890649447691 0.01062810063722730188 0.48472854045627822295 0.48795095623978190780 0.00032508303858300066 0.51172396072163517378 0.49273360783177866384 0.03185613233234574349 0.47541025983587564818 0.49075081269029041664 0.00043182816413278401 0.50881735914557668643 0.51236233643387329995 0.01050799870797843559 0.47712966485814828355 0.51939186110717183720 0.00638063180499700081 0.47422750708783106832 0.49685157861691658931 0.00000000100000000000 0.50314842038308338346 0.50376251978896124939 0.00609062514993390959 0.49014685506110500235 0.50469879197514677660 0.00000000100000000000 0.49530120702485330719 0.48806858812981018803 0.00000000100000000000 0.51193141087018978475 0.49345173654735252633 0.00767168036095551131 0.49887658309169191639 0.51926063211476558568 0.00000000100000000000 0.48073936688523438709 0.49182360714466144547 0.00000000100000000000 0.50817639185533869384 0.50012065040991493525 0.00101172020552988784 0.49886762938455525562 0.49490771372946151807 0.00000000100000000000 0.50509228527053839919 0.50981594186492362741 0.01168450085559137597 0.47849955727948501050 0.48459184220397827358 0.00000007440008454733 0.51540808339593724430 0.51153925961371649045 0.00045999176804108893 0.48800074861824249695 0.49380129779182529992 0.00214174101547949525 0.50405696119269527422 0.10504303642339951619 0.45848347542219436423 0.43647348815440606407 0.09383999674587484296 0.44580529318052469767 0.46035471007360045936 0.11801124345951279071 0.44619343422410290279 0.43579532231638429263 0.10150817897299509174 0.44474184109029252232 0.45374997993671234431 0.14144944553914898244 0.47426718065022838156 0.38428337381062249722 0.08656596263718574491 0.47201374694852676894 0.44142029041428754166 0.10422682420288104099 0.45665008652196642513 0.43912308927515242285 0.07422281507005458467 0.46668026430253822801 0.45909692062740725671 0.11152984148911383733 0.44326164444242566187 0.44520851406846068121 0.12101900721666984662 0.45534926548479054409 0.42363172729853953991 0.19287147372937366030 0.40220634979635128126 0.40492217647427497518 0.19868166550667537562 0.39952077624337684059 0.40179755824994778379 0.20144056442189406386 0.40552701281654912613 0.39303242276155692103 0.17400131741109717276 0.41572345587205422612 0.41027522671684846234 0.19363830614785534912 0.39941552029693161430 0.40694617355521295332 0.20932370419936904837 0.41063785306931777086 0.38003844273131326403 0.21496306930156286463 0.41077627378883840858 0.37426065690959875454 0.20887311245081657818 0.39219787302656328176 0.39892901452262014006 0.18789467459437667052 0.42880445734573224836 0.38330086805989094234 0.21467435158258502126 0.41396326091136687042 0.37136238750604805281 0.30215275924600598634 0.35114326369103593395 0.34670397706295807971 0.27985580964526363124 0.36766711333486662427 0.35247707701986974449 0.29214764907998119758 0.34353124024041165052 0.36432111067960715189 0.28098186396660507214 0.35436535705487937076 0.36465277897851555711 0.29909659519210785028 0.34708664349540557792 0.35381676131248662731 0.29960230758566036569 0.34764467237891033546 0.35275302003542929885 0.28690707484319816212 0.36958476358894237768 0.34350816156785934918 0.31218824558522878521 0.35988855578362860532 0.32792319863114272049 0.29371283648699086921 0.34536893102077848017 0.36091823249223065062 0.32028624797598659324 0.35059182523172049972 0.32912192679229296255 0.39315538655109805166 0.30778919233772789044 0.29905542111117405790 0.39625700997625840083 0.29350948690034872612 0.31023350312339292856 0.40087160410050781678 0.31851581382017457589 0.28061258207931755182 0.40117357253398744366 0.30569836130272198815 0.29312806616329067921 0.40013703551439627759 0.28691859513594913933 0.31294436934965452757 0.39131222513930874474 0.30759794867682349606 0.30108982618386764818 0.40826221599444090238 0.30658973748486684219 0.28514804652069231095 0.41420080477834714250 0.28227625784283560950 0.30352293737881719249 0.39119930707342420728 0.32102763805993583812 0.28777305486664006562 0.37635520411942069430 0.29805329179310008358 0.32559150408747933314 0.51400585200303006150 0.26100245041580294458 0.22499169758116702167 0.50336119658518030384 0.25110166586697690860 0.24553713754784287082 0.47299237773462793344 0.26084178003823194070 0.26616584222714018138 0.49359314224598493936 0.26013978211456978418 0.24626707563944530421 0.52795469779405246324 0.26499345968140075591 0.20705184252454675309 0.48219467330650939152 0.25987283477635270135 0.25793249191713785162 0.47626160019217189667 0.25351817092177358903 0.27022022888605456981 0.51617477226059282902 0.23162353057460718930 0.25220169716479995392 0.49698887507445854705 0.24557159475841641716 0.25743953016712495252 0.52733914260860248469 0.25309832534801629533 0.21956253204338116447 0.56749881833694781896 0.19172441472755546998 0.24077676693549673881 0.59339160859286765870 0.19241414198845174788 0.21419424941868048240 0.62308540846251914136 0.18054125203843729430 0.19637333949904353658 0.59485531592769125275 0.20909554531024135415 0.19604913876206744860 0.61310545246842529377 0.20645329445333451823 0.18044125307824007698 0.60102956519838679483 0.21237444166376903687 0.18659599313784405727 0.59278179178128642679 0.20826418834431797977 0.19895401987439562119 0.60456224253100432353 0.20686687908046738626 0.18857087838852840123 0.59417710257213784963 0.21264514488765640099 0.19317775254020574938 0.59059286756608764257 0.21451811369415349495 0.19488901873975889023 0.69484036887292865980 0.14634823390637874407 0.15881139722069256837 0.69945423984127830241 0.16333221995631252987 0.13721354020240922322 0.69115689116107958956 0.14927316115273414621 0.15956994768618620872 0.68851717088680941536 0.14201541767923545057 0.16946741143395496754 0.69288781352263861812 0.14270021794166909412 0.16441196853569234326 0.68819873910998985433 0.16242980538224471854 0.14937145550776548264 0.68619763716276405141 0.14370194479775053042 0.17010041803948539041 0.68596343194490616568 0.16051691534743553480 0.15351965270765843830 0.70684340251150390433 0.16654037983665334610 0.12661621765184280508 0.70657158115262697073 0.14984891346689468983 0.14357950538047842270 0.79161214498168253062 0.10430887542937690438 0.10407897958894059276 0.79477141808375573184 0.10274451187208989700 0.10248407004415439892 0.80425538032447896342 0.10720945367236509038 0.08853516600315590457 0.79445836435866723502 0.11481368508653701233 0.09072795055479568327 0.80626524450581027459 0.08599284906042292675 0.10774190643376663212 0.77991736902186048486 0.08777798585427237787 0.13230464512386716502 0.77897241390666871474 0.11419808069913564563 0.10682950539419577840 0.80225596727756287585 0.10739115862914316857 0.09035287409329402497 0.81035643868218754093 0.11405964018980654928 0.07558392112800596530 0.80474324803558927588 0.09992219310105134034 0.09533455886335934215 0.89147290804053958002 0.05818869713285088757 0.05033839482660958098 0.87135519951168793895 0.04885203404408157424 0.07979276644423052844 0.90273220877706750187 0.05642671780738096193 0.04084107341555152232 0.90299890240805003039 0.05982401615206547896 0.03717708143988454617 0.88622329583732417646 0.03227381365259313073 0.08150289051008267893 0.89149278212958615875 0.03556871666107842139 0.07293850120933542680 0.90540444756330573650 0.06637446770308205735 0.02822108473361228942 0.89581315874618450135 0.06675457610008654619 0.03743226515372900798 0.86941364504212315101 0.03330392614486758773 0.09728242881300920575 0.88098981477392690476 0.04673780362475228600 0.07227238160132080924
Plot results
Plot in the order of the input file.
admix<-t(as.matrix(read.table("myoutfiles.qopt")))
barplot(admix,col=1:3,space=0,border=NA,xlab="Individuals",ylab="admixture")
Plot using a population label file.
pop<-read.table("pop.info",as.is=T)
admix<-t(as.matrix(read.table("myoutfiles.qopt")))
admix<-admix[,order(pop[,1])]
pop<-pop[order(pop[,1]),]
h<-barplot(admix,col=1:3,space=0,border=NA,xlab="Individuals",ylab="admixture")
text(tapply(1:nrow(pop),pop[,1],mean),-0.05,unique(pop[,1]),xpd=T)
Citation
http://www.genetics.org/content/early/2013/09/03/genetics.113.154138.full.pdf
Bibtex
% 24026093
@Article{pmid24026093,
Author="Skotte, L. and Korneliussen, T. S. and Albrechtsen, A. ",
Title="{{E}stimating {I}ndividual {A}dmixture {P}roportions from {N}ext {G}eneration {S}equencing {D}ata}",
Journal="Genetics",
Year="2013",
Pages=" ",
Month="Sep"
}
Log
- v32 june 25-2013; modified code such that it now compiles on OSX
- v31 june 24-2013; First public version.

